おうちで出来る楽しい理科実験 ~タイルの敷き詰め問題「たった1つのパーツで、周期性を持たせないで隙間なく並べるには?」~
(2025年5月15日)
今回は、ちょっとムズカシイ数学(図形)に関する「実験」である。ただ一つのパーツ(タイル基礎部品)で平面全体を隙間なく敷き詰める「タイル模様問題」を扱う。ここで「周期性」とは図形を並行移動すると元の形にピッタリはまることをいう。このテーマは周期性を持たせるならば簡単なことである。実際、正方形、正三角形、正六角形で可能だ。図1は正六角形の例である。(正方形、正三角形は描くまでもないであろう。)
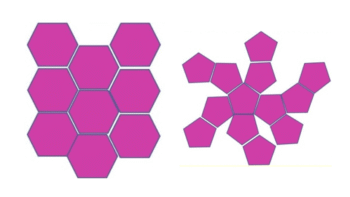
図1.(左) 正六角形、図2.(右) 正五角形での敷詰めの場合
しかし、周期性を与えないで隙間なく敷き詰めることはできるのだろうか?そうなると、三角、四角、六角の間にある、正五角形を基盤にして考えてみるのが自然だ。すると、図2のように必ず発生する隙間を埋める作業が必要になる。だから二つ以上のパーツが必須と思えてくる。
そのような議論展開に基づいて1974年、ロジャー ペンローズ(Roger Penrose)は「五角形に基づく非周期的敷き詰めは二つのパーツで可能になる」として、図3のように、カイト(凧)とダート(矢)という二つの基本図形で成り立つことを示した[1、2]。読者へは、画用紙でカイトとダートを多数作って並べてみることをすすめる。面内での一回り(360°回転)の5分の1(72°回転)で同じ模様になることを5回対称というが、それは図形の中心(赤い円環(えんかん))に対してのみである。
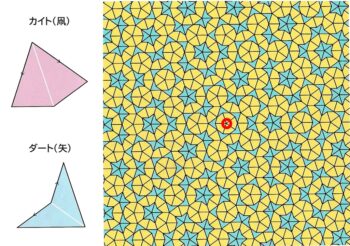
図3. ペンローズによる五角形に基づく非周期的敷き詰め
カイト(凧)とダート(矢)という二つの基本図形で成り立つ
図の中に正五角形(正十角形)は沢山あるが、全体の対称性からはずれている。そのため図形をずらしても重ね合わせることは出来ない。つまり、非周期的な敷き詰めというわけだ。この考え方は3次元において5回対称性を持つ「準結晶」の概念作りに貢献した。実際、固体物性物理では「準結晶」という新しい分野が出来ている[3]。この「準五角形敷き詰め模様」は、当初「ペンローズの発明(発見)」とされたが、30年以上経った2007年に、ポール スタインハーツ(Paul Steinhart)とピタ― ルウ(Peter Lou)が、16世紀に建立されたイランのイスラム寺院(モスク)にあるスパンドレル(壁面の一部)のタイル模様に等価なものがあることを見つけた。数理学者よりタイル職人(の経験)が約500年も先をいっていたわけだ。
そうなると、周期的な敷き詰めのできる正方形と正六角形の中間である正五角形だからこそ、うまく敷き詰められたのであって、この研究を越えて、ただ一つのパーツでの非周期的な敷き詰めはとても不可能ということで決着と思われた。ところが、2023年に、自称「図形愛好家」のデイビッド スミス(David Smith)と計算機実験のグループによって、図4にあげた亀型(Turtle)幽霊(Spectre)パーツが発見された[1、4]。
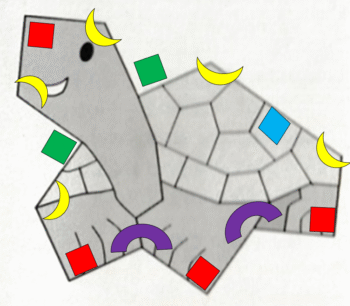
この形は、辺の長さが長短の2種類ある不思議な13角形だが、長い辺の中心を180°角の「頂点」と見なすと等辺14角形(一つの180°角を含む)である。各頂点の角度は90°が(赤四角のように)4つ、180°が(青四角)1つ、270°が(緑四角)2つの他は120°(黄色三日月)が5つ、240°(紫アーチ)が2つである。四角形と六角形の性格を兼ねそなえつつ、2つ加えて360°になる組み合わせが多数用意されていている。その結果、図5のような非周期的で隙間のない敷き詰めが可能になっている。

図5. 亀型(Turtle)幽霊(Spectre)パーツの形は、非周期的で隙間のない敷き詰めができる。
詳細にみると、十文字形の交差境界を持つパーツ(空色の菱形をつけてある)の並び方は、乱雑と見える模様のなかで、かなりの擬似的な6回対称が浮かび上がってくる。「準規則性」があると思われる。読者へは、画用紙でこの亀を多数作って並べて「実験」してみることをすすめる。筆者は、現在3Dプリンターで作った300個で準規則の確認作業をしているが大変興味深い。
さて、この亀型幽霊パーツの他には「解」がないのだろうか?「存在すること」の証明は、一例をあげればよいが、「存在しないこと」の証明は極めて難しい。非周期的なタイル敷き詰め問題の奥は深い。

【おまけ】プリントして、敷詰めてみよう。平面に隙間なく並べることが出来たら、あなたは2023年発見の数学上の新図形課題と同じことをしている!
【参考】
[1]谷岡一郎、荒木義明「ペンローズの幾何学」(講談社BLUE BACKS -2264、2024)
[2]巴山竜来「数学から創るジェネラティブアート-Processingで学ぶかたちのデザイン」(技術評論社)
[2]佐藤憲昭、石政勉「準結晶の科学~構造と物性」(名古屋大学出版会)
[3]David.Smith et al (2023) “A chairal aperiodic monotile”,preprint, https://arxiv.org/abs/2305.17743.

夏目 雄平(なつめ ゆうへい)
千葉大学名誉教授・グランドフェロー(国際教育センター)。固体物性物理学専攻。最近の著書に「やさしく物理」(朝倉書店)、「やさしい化学物理~化学と物理の境界をめぐる」 (朝倉書店)など。 「理科の探検」 (SAMA 企画)編集委員など。文系の著書に「小さい駅の小さな旅案内」 (洋泉社新書)など。各地でサイエンスイベントを行っている。NHK-TV「世界オモシロ学者のスゴ動画祭」に2回出演。
質問は何でも次へして下さい→https://www.facebook.com/yuhei.natsume.1